Разноцветный шестиугольник
*
Центры O1, O2 и O3 трёх непересекающихся окружностей одинакового радиуса расположены в вершинах треугольника. Из точек O1, O2, O3 проведены касательные к данным окружностям так, как показано на рисунке:
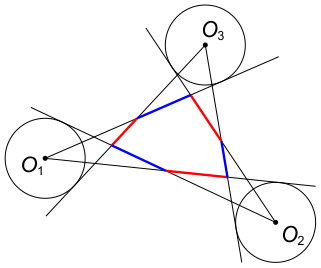
Известно, что эти касательные, пересекаясь, образовали выпуклый шестиугольник, стороны которого через одну покрашены в красный и синий цвета. Докажите, что сумма длин красных отрезков равна сумме длин синих отрезков.
Введём обозначения, как показано на рисунке:
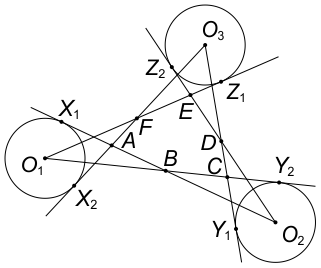
Прямоугольные треугольники O1FX2 и O3Z1F равны между собой, поскольку
Отсюда следует, что
X1B = BY2, Y1D = DZ2 и Z1F = FX2,
что можно переписать следующим образом:
X1A + AB = BC + CY2,
Y1C + CD = DE + EZ2,
Z1E + EF = FA + AX2.
Сложив полученные равенства и заметив, что
X1A = AX2, Y1C = CY2 и Z1E = EZ2
(как отрезки касательных, проведённых к окружности из одной точки), получим:
AB + CD + EF = BC + DE + FA,
что и требовалось доказать.

Комментарии
Thanks for that! It's just the answer I neddee.
Добавить комментарий