Отрезок и луч
*
Опубликовано:
03.01.2012
Категория:
Сложность:
Точка C — середина отрезка AB. На произвольном луче, проведённом из точки C и не лежащем на прямой AB, выбраны три последовательные точки P, M и Q так, что PM = MQ:
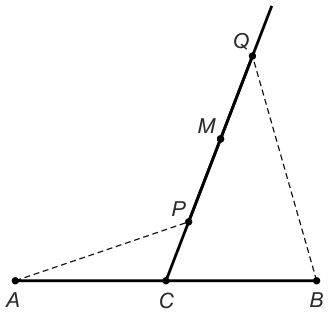
Докажите, что AP + BQ > 2CM.
Решение
Построим параллелограмм CBB'C' таким образом, что CP = C'Q:
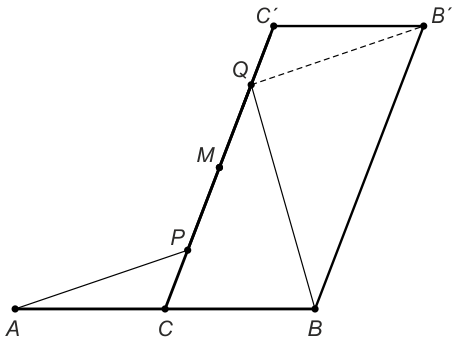
Поскольку в параллелограммах противоположные стороны равны, то C'B' = CB = AC. Значит, треугольники ACP и B'C'Q равны по признаку равенства двух сторон и углу между ними. Следовательно, AP = B'Q.
Поскольку в треугольнике сумма длин двух любых сторон больше длины третьей, то
AP + BQ = QB' + BQ > BB' = CC' = 2CM.

Добавить комментарий