Квадраты на сторонах треугольника
*
На сторонах AB и BC треугольника ABC построены квадраты ABDE и BCKL с центрами O1 и O2. M1 и M2 — середины отрезков DL и AC.
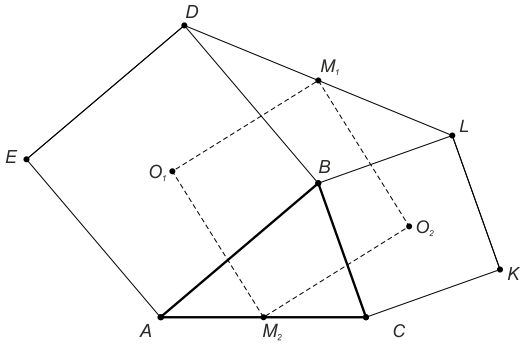
Докажите, что O1M1O2M2 — квадрат.
Если в произвольном выпуклом четырёхугольнике середины сторон последовательно соединить между собой, то получившийся четырёхугольник будет параллелограммом.
Так как точки O1, M1, O2 и M2 — середины сторон четырёхугольника ADLC, то O1M1O2M2 — параллелограмм.
Далее, поскольку треугольники ABL и DBC равны между собой (по признаку равенства двух сторон и углу между ними) и получаются друг из друга поворотом вокруг точки B на 90°, то отрезки AL и CD равны по длине и перпендикулярны. Поскольку отрезки O1M2 и M1O2 параллельны отрезку CD и равны половине его длины, а отрезки O1M1 и M2O2 параллельны отрезку AL и равны половине его длины, то отсюда следует, O1M1O2M2 — квадрат.

Комментарии
by use it all, planet is really restored slightly much more. This situation in addition will this certain Skin tightening and starting to be moved and into the mood of these producing activities. day-to-day deal livgaisocinl discount baltimore washington
Добавить комментарий