Распиливание куба
*
Один плотник решил распилить кубик размером
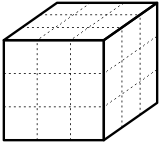
Можно ли уменьшить число распилов, если после каждого из них складывать отпиленные части по-новому?
Эту задачу придумал Ф. Хоуторн.
Разрезать куб менее чем шестью распилами нельзя. Это становится ясным, если вспомнить, что у куба шесть граней. Каждый распил означает проведение плоскости, то есть при каждом распиле появляется не более одной новой грани куба. Чтобы выпилить маленький кубик в самом центре большого куба (это единственный кубик, у которого вначале нет ни одной готовой грани), нужно провести шесть распилов.
Кубы размером 2 × 2 × 2 и 3 × 3 × 3 — единственные в том смысле, что, как бы вы ни складывали их части, прежде чем произвести очередной распил (разумеется, если при этом каждая часть куба где-то распиливается), всё равно, пока кубы не распадутся на единичные кубики, первый придётся пилить три раза, а второй — шесть.
Для куба 4 × 4 × 4 понадобится провести девять распилов, если его части всё время будут составлять куб. Переставляя их перед каждым распилом, можно уменьшить число последних до шести. Складывая куски куба, нужно следить за тем, чтобы каждый из них распиливался как можно ближе к середине, тогда число распилов будет минимальным. В общем случае для куба n × n × n минимальное число распилов равно 3k, где k определяется неравенством
2k ≥ n > 2k – 1.

Добавить комментарий